Redis 数据结构

Redis 为什么那么快？

除了它是内存数据库，使得所有的操作都在内存上进行之外，还有一个重要因素，它实现的数据结构，使得我们对数据进行增删查改操作时，Redis 能高效的处理。

键值对数据库是怎么实现的？

Redis 的键值对中的 key 就是字符串对象，而 value 可以是字符串对象，也可以是集合数据类型的对象，比如 List 对象、Hash 对象、Set 对象和 Zset 对象。

Redis 是使用了一个「哈希表」保存所有键值对，哈希表的最大好处就是让我们可以用 O(1) 的时间复杂度来快速查找到键值对。哈希表其实就是一个数组，数组中的元素叫做哈希桶。

哈希桶存放的是指向键值对数据的指针（dictEntry*），这样通过指针就能找到键值对数据，保存了 void * key 和 void * value 指针，分别指向了实际的键对象和值对象，这样一来，即使值是集合数据，也可以通过 void * value 指针找到。

我这里画了一张 Redis 保存键值对所涉及到的数据结构。

这里先大概说下图中涉及到的数据结构的名字和用途：

• redisDb 结构，表示 Redis 数据库的结构，结构体里存放了指向了 dict 结构的指针；

  • 总体数据库结构

• dict 结构，结构体里存放了 2 个哈希表，正常情况下都是用「哈希表 1」，「哈希表 2」只有在 rehash 的时候才用；

• ditctht 结构，表示哈希表的结构，结构里存放了哈希表数组，数组中的每个元素都是指向一个哈希表节点结构（dictEntry）的指针；

• dictEntry 结构，表示哈希表节点的结构，结构里存放了 **void * key 和 void * value 指针， key 指向的是 String 对象，而 value 则可以指向 String 对象，也可以指向集合类型的对象，比如 List 对象、Hash 对象、Set 对象和 Zset 对象。

特别说明下，void * key 和 void * value 指针指向的是 Redis 对象，Redis 中的每个对象都由 redisObject 结构表示，如下图：

对象结构里包含的成员变量：

• type，标识该对象是什么类型的对象（String 对象、List 对象、Hash 对象、Set 对象和 Zset 对象）；
• encoding，标识该对象使用了哪种底层的数据结构；
• ptr，指向底层数据结构的指针。

我画了一张 Redis 键值对数据库的全景图，你就能清晰知道 Redis 对象和数据结构的关系了：

SDS

Redis 是用 C 语言实现的，但是它没有直接使用 C 语言的 char* 字符数组来实现字符串，而是自己封装了一个名为简单动态字符串（simple dynamic string，SDS）的数据结构来表示字符串，也就是 Redis 的 String 数据类型的底层数据结构是 SDS。

C 语言字符串的缺陷

• 获取字符串长度的时间复杂度为 O（N）；
• 字符串的结尾是以“\0”字符标识，字符串里面不能包含有“\0”字符，因此不能保存二进制数据；
• 字符串操作函数不高效且不安全，比如有缓冲区溢出的风险，有可能会造成程序运行终止；

SDS 结构设计

下图就是 Redis 5.0 的 SDS 的数据结构：

结构中的每个成员变量分别介绍下：

• len，记录了字符串长度。

  • 在获取字符串长度的时候，直接返回这个成员变量的值就行，所以复杂度只有 O（1）。

• alloc，分配给字符数组的空间长度。

  • alloc 和 len 成员变量让SDS API 通过 alloc - len 计算剩余可用的空间大小，在对字符串做修改操作的时候，就可以由程序内部判断缓冲区大小是否足够用。当判断出缓冲区大小不够用时，Redis 会自动将扩大 SDS 的空间大小。

    • 如果所需的 sds 长度小于 1 MB，那么最后的扩容是按照翻倍扩容来执行的，即 2 倍的 newlen

    • 如果所需的 sds 长度超过 1 MB，那么最后的扩容长度应该是 newlen + 1MB。

• flags，用来表示不同类型的 SDS。一共设计了 5 种类型，分别是 sdshdr5、sdshdr8、sdshdr16、sdshdr32 和 sdshdr64，后面在说明区别之处。

  • 灵活保存不同大小的字符串，从而有效节省内存空间。

• buf[]，字符数组，用来保存实际数据。

  • SDS 的 API 都是以处理二进制的方式来处理 SDS 存放在 buf[] 里的数据，程序不会对其中的数据做任何限制，数据写入的时候时什么样的，它被读取时就是什么样的。因此除了文本数据还能保存任意格式的二进制数据。

• Redis 在编程上还告诉编译器取消结构体在编译过程中的优化对齐，按照实际占用字节数进行对齐，因此占用空间小，效率高

---

链表

Redis 的 List 对象的底层实现之一就是链表。C 语言本身没有链表这个数据结构的，所以 Redis 自己设计了一个链表数据结构。

• Redis 链表是一个双向链表

---

压缩列表

压缩列表结构设计

压缩列表是 Redis 为了节约内存而开发的，它是由连续内存块组成的顺序型数据结构，有点类似于数组。

压缩列表在表头有三个字段：

• zlbytes，记录整个压缩列表占用的内存字节数；
• zltail，记录压缩列表「尾部」节点距离起始地址由多少字节，也就是列表尾的偏移量；
• zllen，记录压缩列表包含的节点数量；
• zlend，标记压缩列表的结束点，固定值 0xFF（十进制 255）。

在压缩列表中，如果我们要查找定位第一个元素和最后一个元素，可以通过表头三个字段（zllen）的长度直接定位，复杂度是 O(1)。而查找其他元素时，就没有这么高效了，只能逐个查找，此时的复杂度就是 O(N) 了，因此压缩列表不适合保存过多的元素。

另外，压缩列表节点（entry）的构成如下：

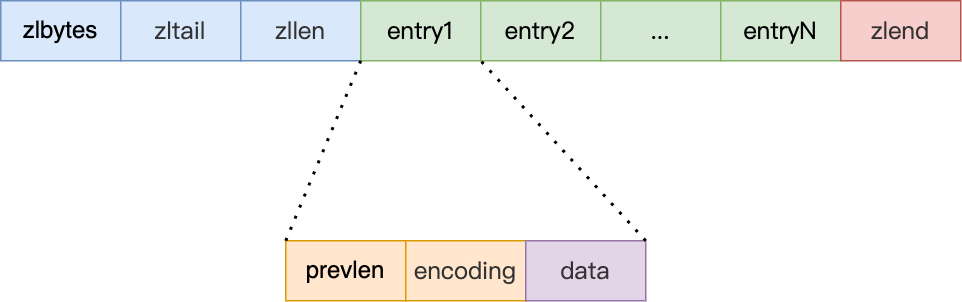
压缩列表节点包含三部分内容：

• prevlen，记录了「前一个节点」的长度，目的是为了实现从后向前遍历；
• encoding，记录了当前节点实际数据的「类型和长度」，类型主要有两种：字符串和整数。
• data，记录了当前节点的实际数据，类型和长度都由 encoding 决定；

当我们往压缩列表中插入数据时，压缩列表就会根据数据类型是字符串还是整数，以及数据的大小，会使用不同空间大小的 prevlen 和 encoding 这两个元素里保存的信息，这种根据数据大小和类型进行不同的空间大小分配的设计思想，正是 Redis 为了节省内存而采用的。

分别说下，prevlen 和 encoding 是如何根据数据的大小和类型来进行不同的空间大小分配。

压缩列表里的每个节点中的 prevlen 属性都记录了「前一个节点的长度」，而且 prevlen 属性的空间大小跟前一个节点长度值有关，比如：

• 如果前一个节点的长度小于 254 字节，那么 prevlen 属性需要用 1 字节的空间来保存这个长度值；
• 如果前一个节点的长度大于等于 254 字节，那么 prevlen 属性需要用 5 字节的空间来保存这个长度值；

encoding 属性的空间大小跟数据是字符串还是整数，以及字符串的长度有关：

• 如果当前节点的数据是整数，则 encoding 会使用 1 字节的空间进行编码。通过 encoding 确认了整数类型，就可以确认整数数据的实际大小了，比如如果 encoding 编码确认了数据是 int16 整数，那么 data 的长度就是 int16 的大小。
• 如果当前节点的数据是字符串，根据字符串的长度大小，encoding 会使用 1 字节/2 字节/5 字节的空间进行编码，encoding 编码的前两个 bit 表示数据的类型，后续的其他 bit 标识字符串数据的实际长度，即 data 的长度。

连锁更新

压缩列表除了查找复杂度高的问题，还有一个问题。

压缩列表新增某个元素或修改某个元素时，如果空间不够，压缩列表占用的内存空间就需要重新分配。而当新插入的元素较大时，可能会导致后续元素的 prevlen 占用空间都发生变化，从而引起「连锁更新」问题，导致每个元素的空间都要重新分配，造成访问压缩列表性能的下降。

现在假设一个压缩列表中有多个连续的、长度在 250～253 之间的节点，如下图：

因为这些节点长度值小于 254 字节，所以 prevlen 属性需要用 1 字节的空间来保存这个长度值。

这时，如果将一个长度大于等于 254 字节的新节点加入到压缩列表的表头节点，即新节点将成为 e1 的前置节点，如下图：

因为 e1 节点的 prevlen 属性只有 1 个字节大小，无法保存新节点的长度，此时就需要对压缩列表的空间重分配操作，并将 e1 节点的 prevlen 属性从原来的 1 字节大小扩展为 5 字节大小。

多米诺牌的效应就此开始。

e1 原本的长度在 250～253 之间，因为刚才的扩展空间，此时 e1 的长度就大于等于 254 了，因此原本 e2 保存 e1 的 prevlen 属性也必须从 1 字节扩展至 5 字节大小。

正如扩展 e1 引发了对 e2 扩展一样，扩展 e2 也会引发对 e3 的扩展，而扩展 e3 又会引发对 e4 的扩展…… 一直持续到结尾。

这种在特殊情况下产生的连续多次空间扩展操作就叫做「连锁更新」。

因此，压缩列表只会用于保存的节点数量不多的场景，只要节点数量足够小，即使发生连锁更新，也是能接受的。

哈希表

哈希表中的每一个 key 都是独一无二的。Hash 对象的实现之一就是哈希表。

哈希表优点在于，它能以 O(1) 的复杂度快速查询数据。

但是在哈希表大小固定的情况下，随着数据不断增多，那么哈希冲突的可能性也会越高。

Redis 采用了「链式哈希」来解决哈希冲突。

哈希表结构设计

Redis 的哈希表结构如下：

typedef struct dictht {
    //哈希表数组
    dictEntry **table;
    //哈希表大小
    unsigned long size;  
    //哈希表大小掩码，用于计算索引值
    unsigned long sizemask;
    //该哈希表已有的节点数量
    unsigned long used;
} dictht;

可以看到，哈希表是一个数组（dictEntry **table），数组的每个元素是一个指向「哈希表节点（dictEntry）」的指针。

哈希表节点的结构如下：

typedef struct dictEntry {
    //键值对中的键
    void *key;
  
    //键值对中的值
    union {
        void *val;
        uint64_t u64;
        int64_t s64;
        double d;
    } v;
    //指向下一个哈希表节点，形成链表
    struct dictEntry *next;
} dictEntry;

dictEntry 结构里不仅包含指向键和值的指针，还包含了指向下一个哈希表节点的指针，这个指针用来实现链式哈希。被分配到同一个哈希桶上的多个节点可以用这个单项链表连接起来，当链表长度太长会导致出现O(n)时间复杂度

Redis不使用红黑树解决冲突是因为红黑树比较复杂，且红黑树的节点相比链表占用内存更多，维护也较为复杂

dictEntry 结构里键值对中的值是一个「联合体 v」定义，因为当「值」是整数或浮点数时，就可以将值的数据内嵌在 dictEntry 结构里，无需再用一个指针指向实际的值，从而节省了内存空间，当值是结构体时使用指针。

rehash

在正常服务请求阶段，插入的数据，都会写入到「哈希表 1」，此时的「哈希表 2」并没有被分配空间。

随着数据逐步增多，触发了 rehash 操作，这个过程分为三步：

• 给「哈希表 2」分配空间，一般会比「哈希表 1」大 2 倍；

• 将「哈希表 1」的数据迁移到「哈希表 2」中；

  • 如果「哈希表 1」的数据量非常大，那么在迁移至「哈希表 2」的时候，因为会涉及大量的数据拷贝，此时可能会对 Redis 造成阻塞，无法服务其他请求

• 迁移完成后，「哈希表 1」的空间会被释放，并把「哈希表 2」设置为「哈希表 1」，然后在「哈希表 2」新创建一个空白的哈希表，为下次 rehash 做准备。

渐进式 rehash

Redis 采用了渐进式 rehash，将数据的迁移的工作分多次迁移。

渐进式 rehash 步骤如下：

• 给「哈希表 2」分配空间；
• 在 rehash 进行期间，每次哈希表元素进行新增、删除、查找或者更新操作时，Redis 除了会执行对应的操作之外，还会顺序将「哈希表 1」中索引位置上的所有 key-value 迁移到「哈希表 2」上；
• 随着处理客户端发起的哈希表操作请求数量越多，最终在某个时间点会把「哈希表 1」的所有 key-value 迁移到「哈希表 2」，从而完成 rehash 操作。
• 没有文章显示的说明如果已知不rehash结束怎么办
  • 可以设置超时时间，超时通过每次请求必定复制一个key的所有数据到hash2，这样一定可以复制完
  • 或者闲时复制

避免了一次性 rehash 的耗时操作。

在进行渐进式 rehash 的过程中，哈希表元素的删除、查找、更新等操作都会在这两个哈希表进行。

比如，查找一个 key 的值的话，先会在「哈希表 1」里面进行查找，如果没找到，就会继续到哈希表 2 里面进行找到。

另外，在渐进式 rehash 进行期间，新增一个 key-value 时，会被保存到「哈希表 2」里面，而「哈希表 1」则不再进行任何添加操作，这样保证了「哈希表 1」的 key-value 数量只会减少，随着 rehash 操作的完成，最终「哈希表 1」就会变成空表。

rehash 触发条件

rehash 的触发条件跟**负载因子（load factor）**有关系。

负载因子可以通过下面这个公式计算：

触发 rehash 操作的条件，主要有两个：

• 当负载因子大于等于 1，并且 Redis 没有在执行 bgsave 命令或者 bgrewiteaof 命令，也就是没有执行 RDB 快照或没有进行 AOF 重写的时候，就会进行 rehash 操作。
• 当负载因子大于等于 5 时，此时说明哈希冲突非常严重了，不管有没有有在执行 RDB 快照或 AOF 重写，都会强制进行 rehash 操作。

整数集合

整数集合是 Set 对象的底层实现之一。当一个 Set 对象只包含整数值元素，并且元素数量不大时，就会使用整数集这个数据结构作为底层实现。

整数集合结构设计

整数集合本质上是一块连续内存空间，它的结构定义如下：

typedef struct intset {
    //编码方式
    uint32_t encoding;
    //集合包含的元素数量
    uint32_t length;
    //保存元素的数组
    int8_t contents[];
} intset;

可以看到，保存元素的容器是一个 contents 数组，contents 数组的真正类型取决于 intset 结构体里的 encoding 属性的值。比如：

• 如果 encoding 属性值为 INTSET_ENC_INT16，那么 contents 就是一个 int16_t 类型的数组，数组中每一个元素的类型都是 int16_t（还有int32_t，int64_t）；

整数集合的升级操作

当我们将一个新元素加入到整数集合里面，如果新元素的类型（int32_t）比整数集合现有所有元素的类型（int16_t）都要长时，整数集合需要先进行升级，也就是按新元素的类型（int32_t）扩展 contents 数组的空间大小，将数据按照原来集合的有序性重新安放，然后才能将新元素加入到整数集合里。

整数集合升级的过程不会重新分配一个新类型的数组，而是在原本的数组上扩展空间，然后在将每个元素按间隔类型大小分割，如果 encoding 属性值为 INTSET_ENC_INT16，则每个元素的间隔就是 16 位。

整数集合升级的好处是节省内存资源。

如果一直向整数集合添加 int16_t 类型的元素，那么整数集合的底层实现就一直是用 int16_t 类型的数组，只有在我们要将 int32_t 类型或 int64_t 类型的元素添加到集合时，才会对数组进行升级操作。

整数集合不支持降级操作，一旦对数组进行了升级，就会一直保持升级后的状态。

---

跳表

Redis 只有 Zset 对象的底层实现用到了跳表，跳表的优势是能支持平均 O(logN) 复杂度的节点查找。

zset 结构体里有两个数据结构：一个是跳表，一个是哈希表。这样的好处是既能进行高效的范围查询，也能进行高效单点查询。

typedef struct zset {
    dict *dict;
    zskiplist *zsl;
} zset;

Zset 对象在执行数据插入或是数据更新的过程中，会依次在跳表和哈希表中插入或更新相应的数据，从而保证了跳表和哈希表中记录的信息一致。

Zset 对象能支持范围查询（如 ZRANGEBYSCORE 操作），这是因为它的数据结构设计采用了跳表，而又能以常数复杂度获取元素权重（如 ZSCORE 操作），这是因为它同时采用了哈希表进行索引。

跳表结构设计

图中头节点有 L0~L2 三个头指针，分别指向了不同层级的节点，然后每个层级的节点都通过指针连接起来：

• L0 层级共有 5 个节点，分别是节点 1、2、3、4、5；
• L1 层级共有 3 个节点，分别是节点 2、3、5；
• L2 层级只有 1 个节点，也就是节点 3。

如果我们要在链表中查找节点 4 这个元素，只能从头开始遍历链表，需要查找 4 次，而使用了跳表后，只需要查找 2 次就能定位到节点 4，因为可以在头节点直接从 L2 层级跳到节点 3，然后再往前遍历找到节点 4。

可以看到，这个查找过程就是在多个层级上跳来跳去，最后定位到元素。当数据量很大时，跳表的查找复杂度就是 O(logN)。

那跳表节点是怎么实现多层级的呢？这就需要看「跳表节点」的数据结构了，如下：

typedef struct zskiplistNode {
    //Zset 对象的元素值
    sds ele;
    //元素权重值
    double score;
    //后向指针
    struct zskiplistNode *backward;
  
    //节点的 level 数组，保存每层上的前向指针和跨度
    struct zskiplistLevel {
        struct zskiplistNode *forward;
        unsigned long span;
    } level[];
} zskiplistNode;

Zset 对象要同时保存「元素」和「元素的权重」，对应到跳表节点结构里就是 sds 类型的 ele 变量和 double 类型的 score 变量。每个跳表节点都有一个后向指针（struct zskiplistNode *backward），指向前一个节点，目的是为了方便从跳表的尾节点开始访问节点，这样倒序查找时很方便。

跳表是一个带有层级关系的链表，而且每一层级可以包含多个节点，每一个节点通过指针连接起来，实现这一特性就是靠跳表节点结构体中的zskiplistLevel 结构体类型的 level 数组。

level 数组中的每一个元素代表跳表的一层，也就是由 zskiplistLevel 结构体表示，比如 leve[0] 就表示第一层，leve[1] 就表示第二层。zskiplistLevel 结构体里定义了「指向下一个跳表节点的指针」和「跨度」，跨度时用来记录两个节点之间的距离。

比如，下面这张图，展示了各个节点的跨度。

第一眼看到跨度的时候，以为是遍历操作有关，实际上并没有任何关系，遍历操作只需要用前向指针（struct zskiplistNode *forward）就可以完成了。

跨度实际上是为了计算这个节点在跳表中的排位。具体怎么做的呢？因为跳表中的节点都是按序排列的，那么计算某个节点排位的时候，从头节点点到该结点的查询路径上，将沿途访问过的所有层的跨度累加起来，得到的结果就是目标节点在跳表中的排位。

举个例子，查找图中节点 3 在跳表中的排位，从头节点开始查找节点 3，查找的过程只经过了一个层（L2），并且层的跨度是 3，所以节点 3 在跳表中的排位是 3。

问题来了，由谁定义哪个跳表节点是头节点呢？这就介绍「跳表」结构体了，如下所示：

typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    unsigned long length;
    int level;
} zskiplist;

跳表结构里包含了：

• 跳表的头尾节点，便于在 O(1) 时间复杂度内访问跳表的头节点和尾节点；
• 跳表的长度，便于在 O(1) 时间复杂度获取跳表节点的数量；
• 跳表的最大层数，便于在 O(1) 时间复杂度获取跳表中层高最大的那个节点的层数量；

跳表节点查询过程

查找一个跳表节点的过程时，跳表会从头节点的最高层开始，逐一遍历每一层。在遍历某一层的跳表节点时，会用跳表节点中的 SDS 类型的元素和元素的权重来进行判断，共有两个判断条件：

• 如果当前节点的权重「小于」要查找的权重时，跳表就会访问该层上的下一个节点。
• 如果当前节点的权重「等于」要查找的权重时，并且当前节点的 SDS 类型数据「小于」要查找的数据时，跳表就会访问该层上的下一个节点。

如果上面两个条件都不满足，或者下一个节点为空时，跳表就会使用目前遍历到的节点的 level 数组里的下一层指针，然后沿着下一层指针继续查找，这就相当于跳到了下一层接着查找。

举个例子，下图有个 3 层级的跳表。

如果要查找「元素：abcd，权重：4」的节点，查找的过程是这样的：

• 先从头节点的最高层开始，L2 指向了「元素：abc，权重：3」节点，这个节点的权重比要查找节点的小，所以要访问该层上的下一个节点；
• 但是该层的下一个节点是空节点（leve[2]指向的是空节点），于是就会跳到「元素：abc，权重：3」节点的下一层去找，也就是 leve[1];
• 「元素：abc，权重：3」节点的 leve[1] 的下一个指针指向了「元素：abcde，权重：4」的节点，然后将其和要查找的节点比较。虽然「元素：abcde，权重：4」的节点的权重和要查找的权重相同，但是当前节点的 SDS 类型数据「大于」要查找的数据，所以会继续跳到「元素：abc，权重：3」节点的下一层去找，也就是 leve[0]；
• 「元素：abc，权重：3」节点的 leve[0] 的下一个指针指向了「元素：abcd，权重：4」的节点，该节点正是要查找的节点，查询结束。

跳表节点层数设置

跳表的相邻两层的节点数量的比例会影响跳表的查询性能。

举个例子，下图的跳表，第二层的节点数量只有 1 个，而第一层的节点数量有 6 个。

这时，如果想要查询节点 6，那基本就跟链表的查询复杂度一样，就需要在第一层的节点中依次顺序查找，复杂度就是 O(N) 了。所以，为了降低查询复杂度，我们就需要维持相邻层结点数间的关系。

跳表的相邻两层的节点数量最理想的比例是 2:1，查找复杂度可以降低到 O(logN)。

下图的跳表就是，相邻两层的节点数量的比例是 2 : 1。

那怎样才能维持相邻两层的节点数量的比例为 2 : 1 呢？

如果采用新增节点或者删除节点时，来调整跳表节点以维持比例的方法的话，会带来额外的开销。

Redis 则采用一种巧妙的方法是，跳表在创建节点的时候，随机生成每个节点的层数，并没有严格维持相邻两层的节点数量比例为 2 : 1 的情况。

具体的做法是，跳表在创建节点时候，会生成范围为[0-1]的一个随机数，如果这个随机数小于 0.25（相当于概率 25%），那么层数就增加 1 层，然后继续生成下一个随机数，直到随机数的结果大于 0.25 结束，最终确定该节点的层数。

这样的做法，相当于每增加一层的概率不超过 25%，层数越高，概率越低，层高最大限制是 64。

虽然我前面讲解跳表的时候，图中的跳表的「头节点」都是 3 层高，但是其实如果层高最大限制是 64，那么在创建跳表「头节点」的时候，就会直接创建 64 层高的头节点。

如下代码，创建跳表时，头节点的 level 数组有 ZSKIPLIST_MAXLEVEL 个元素（层），节点不存储任何 member 和 score 值，level 数组元素的 forward 都指向 NULL，span 值都为 0。

点击查看完整代码实现

点击查看完整代码实现

/* Create a new skiplist. */
zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}

:::

其中，ZSKIPLIST_MAXLEVEL 定义的是最高的层数，Redis 7.0 定义为 32，Redis 5.0 定义为 64，Redis 3.0 定义为 32。

为什么用跳表而不用平衡树？

这里插一个常见的面试题：为什么 Zset 的实现用跳表而不用平衡树（如 AVL 树、红黑树等）？

主要是从内存占用、对范围查找的支持、实现难易程度这三方面总结的原因：

• 从内存占用上来比较，跳表比平衡树更灵活一些。平衡树每个节点包含 2 个指针（分别指向左右子树），而跳表每个节点包含的指针数目平均为 1/(1-p)，具体取决于参数 p 的大小。如果像 Redis 里的实现一样，取 p=1/4，那么平均每个节点包含 1.33 个指针，比平衡树更有优势。
• 在做范围查找的时候，跳表比平衡树操作要简单。在平衡树上，我们找到指定范围的小值之后，还需要以中序遍历的顺序继续寻找其它不超过大值的节点。如果不对平衡树进行一定的改造，这里的中序遍历并不容易实现。而在跳表上进行范围查找就非常简单，只需要在找到小值之后，对第 1 层链表进行若干步的遍历就可以实现。
• 从算法实现难度上来比较，跳表比平衡树要简单得多。平衡树的插入和删除操作可能引发子树的调整，逻辑复杂，而跳表的插入和删除只需要修改相邻节点的指针，操作简单又快速。

quicklist

其实 quicklist 就是「双向链表 + 压缩列表」组合，因为一个 quicklist 就是一个链表，而链表中的每个元素又是一个压缩列表。

quicklist 通过控制每个链表节点中的压缩列表的大小或者元素个数，来规避连锁更新的问题。因为压缩列表元素越少或越小，连锁更新带来的影响就越小，从而提供了更好的访问性能。

quicklist 结构设计

quicklist 的结构体跟链表的结构体类似，都包含了表头和表尾，区别在于 quicklist 的节点是 quicklistNode。

quicklistNode 结构体里包含了前一个节点和下一个节点指针，这样每个 quicklistNode 形成了一个双向链表。但是链表节点的元素不再是单纯保存元素值，而是保存了一个压缩列表，所以 quicklistNode 结构体里有个指向压缩列表的指针 *zl。

我画了一张图，方便你理解 quicklist 数据结构。

在向 quicklist 添加一个元素的时候，不会像普通的链表那样，直接新建一个链表节点。而是会检查插入位置的压缩列表是否能容纳该元素，如果能容纳就直接保存到 quicklistNode 结构里的压缩列表，如果不能容纳，才会新建一个新的 quicklistNode 结构。

quicklist 会控制 quicklistNode 结构里的压缩列表的大小或者元素个数，来规避潜在的连锁更新的风险，但是这并没有完全解决连锁更新的问题。

listpack

压缩列表连锁更新的问题，来源于它的结构设计，所以要想彻底解决这个问题，需要设计一个新的数据结构，而quicklistNode 还是用了压缩列表来保存元素，并没有完全解决这个问题。

于是，Redis 在 5.0 新设计一个数据结构叫 listpack，目的是替代压缩列表，它最大特点是 listpack 中每个节点不再包含前一个节点的长度了，压缩列表每个节点正因为需要保存前一个节点的长度字段，就会有连锁更新的隐患。

listpack 结构设计

listpack 采用了压缩列表的很多优秀的设计，比如还是用一块连续的内存空间来紧凑地保存数据，并且为了节省内存的开销，listpack 节点会采用不同的编码方式保存不同大小的数据。

我们先看看 listpack 结构：

listpack 头包含两个属性，分别记录了 listpack 总字节数和元素数量，然后 listpack 末尾也有个结尾标识。图中的 listpack entry 就是 listpack 的节点了。

每个 listpack 节点结构如下：

主要包含三个方面内容：

• encoding，定义该元素的编码类型，会对不同长度的整数和字符串进行编码；
• data，实际存放的数据；
• len，encoding+data 的总长度；
  • 通过累加每个节点的len字段值来回溯到前一个节点的起始位置。压缩列表只保存前一个数据的长度，没有保存当前数据的长度，插入的时候只有插入的元素需要变化长度

可以看到，listpack 没有压缩列表中记录前一个节点长度的字段了，listpack 只记录当前节点的长度，当我们向 listpack 加入一个新元素的时候，不会影响其他节点的长度字段的变化，从而避免了压缩列表的连锁更新问题。

---

读者问答

压缩列表的 entry 为什么要保存 prevlen 呢？listpack 改成 len 之后不会影响功能吗？

压缩列表的 entry 保存 prevlen 是为了实现节点从后往前遍历，知道前一个节点的长度，就可以计算前一个节点的偏移量。

listpack 一样可以支持从后往前遍历的。

---